When we render a list without adding key for each item, we would get a warning.

The reason for this is explained pretty nicely on the homepage, but the explanation is conceptual, let’s get hands dirty by looking at how exactly key works internally.

reconcileChildrenArray()

We are already a bit familiar with the code base now, it should not be hard to target the reconcile function for array - reconcileChildrenArray() (source)

if not, you can search on my blog for past entries, or watch my youtube video series

The function body is a bit intimidating, first starting with a long paragraph of comments.

js
// This algorithm can't optimize by searching from both ends since we
// don't have backpointers on fibers. I'm trying to see how far we can get
// with that model. If it ends up not being worth the tradeoffs, we can
// add it later.
// Even with a two ended optimization, we'd want to optimize for the case
// where there are few changes and brute force the comparison instead of
// going for the Map. It'd like to explore hitting that path first in
// forward-only mode and only go for the Map once we notice that we need
// lots of look ahead. This doesn't handle reversal as well as two ended
// search but that's unusual. Besides, for the two ended optimization to
// work on Iterables, we'd need to copy the whole set.
// In this first iteration, we'll just live with hitting the bad case
// (adding everything to a Map) in for every insert/move.

js
// This algorithm can't optimize by searching from both ends since we
// don't have backpointers on fibers. I'm trying to see how far we can get
// with that model. If it ends up not being worth the tradeoffs, we can
// add it later.
// Even with a two ended optimization, we'd want to optimize for the case
// where there are few changes and brute force the comparison instead of
// going for the Map. It'd like to explore hitting that path first in
// forward-only mode and only go for the Map once we notice that we need
// lots of look ahead. This doesn't handle reversal as well as two ended
// search but that's unusual. Besides, for the two ended optimization to
// work on Iterables, we'd need to copy the whole set.
// In this first iteration, we'll just live with hitting the bad case
// (adding everything to a Map) in for every insert/move.

It looks like React is compromising here, NOT doing two ended optimization because we don't have backpointers on fibers.

In the previous entries, we see that for children React holds a linked list of fibers by ‘sibling’ rather than array.

What is two ended optimization? I guess it would be some algorithm which scans from end rather than start. This leads to our first problem.

What kind of changes could happen for a list ?

Suppose we have an array.

js
const arrPrev = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];

js
const arrPrev = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];

After some actions, it becomes a new array. If we find some element at index i is different, there might have many possibilities of modifications.

1. a new element is inserted at index i
2. a new element is replacing the old element at index i
3. an existing element is moved from other index to i
4. an existing element is moved from other index and replaced the old element at index i.
5. old element i is removed, the next element takes the position.
6. …

We can see it is hard to figure out which is the case without extra analysis.

Suppose we have a new array.

js
const arrNext = [11, 12, 9, 4, 7, 16, 1, 2, 3];

js
const arrNext = [11, 12, 9, 4, 7, 16, 1, 2, 3];

How should we transform with minimum cost?

If we care about the minimum moves, it is similar to Levenshtein distance, but after finding the minium moves, we still need to to the transformation.

Total Cost = Cost of analyzing(reconcile) + Cost of transforming (commit changes)

Take an extreme example, what if we reversed the array ?

js
const arrPrev = [10, 9, 8, 7, 6, 5, 4, 3, 2, 1];

js
const arrPrev = [10, 9, 8, 7, 6, 5, 4, 3, 2, 1];

Since each position is different, the analyzing part is going to cost a lot of time to find the optimal moves, which might be better we just replace all of them.

Obviously we can take the dummy approach - treat all different positions as replace with new items.

This helps understand why there is two ended optimization, think about case like below

js
const arrPrev = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];
const arrNext = [11, 12, 7, 8, 9, 10];

js
const arrPrev = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];
const arrNext = [11, 12, 7, 8, 9, 10];

It is hard to infer from head, but if we reverse it

js
const arrPrev = [10, 9, 8, 7, 6, 5, 4, 3, 2, 1];
const arrNext = [10, 9, 8, 7, 6, 12, 11];

js
const arrPrev = [10, 9, 8, 7, 6, 5, 4, 3, 2, 1];
const arrNext = [10, 9, 8, 7, 6, 12, 11];

It looks much clear now. I guess this is the two-way optimization ? maybe I’m wrong.

React’s approach

In order to understand the code below better, let me explain it a bit.

Basically, React constructs new fiber list by following step

1. try optimistically compare the items with same key

   • both starts at index: 0, (headOld, headNew)
   • compare the old fiber and new element
     • if Key is the same, then lucky, memo that we can reconcile it.
     • if not, break

2. for the rest

   • see if we can reuse the old fibers by key
     • if can, use it for future reconcile.
     • if not, create new
   • delete the unused fibers

This means that, once React finds key mismatch, it will try to “move” or “create new fiber”.

Let’s go back to React source code. It starts with a for loop comparing old fibers and new elements.

js
for (; oldFiber !== null && newIdx < newChildren.length; newIdx++) {
  if (oldFiber.index > newIdx) {
    nextOldFiber = oldFiber;
    oldFiber = null;
  } else {
    nextOldFiber = oldFiber.sibling;
  }
  const newFiber = updateSlot(
    returnFiber,
    oldFiber,
    newChildren[newIdx],
    lanes
  );
  if (newFiber === null) {
    // a better way to communicate whether this was a miss or null,
    // boolean, undefined, etc.
    if (oldFiber === null) {
      oldFiber = nextOldFiber;
    }
    break;
  }
  if (shouldTrackSideEffects) {
    if (oldFiber && newFiber.alternate === null) {
      // We matched the slot, but we didn't reuse the existing fiber, so we
      // need to delete the existing child.
      deleteChild(returnFiber, oldFiber);
    }
  }
  lastPlacedIndex = placeChild(newFiber, lastPlacedIndex, newIdx);
  if (previousNewFiber === null) {
    // TODO: Move out of the loop. This only happens for the first run.
    resultingFirstChild = newFiber;
  } else {
    // TODO: Defer siblings if we're not at the right index for this slot.
    // I.e. if we had null values before, then we want to defer this
    // for each null value. However, we also don't want to call updateSlot
    // with the previous one.
    previousNewFiber.sibling = newFiber;
  }
  previousNewFiber = newFiber;
  oldFiber = nextOldFiber;
}

js
for (; oldFiber !== null && newIdx < newChildren.length; newIdx++) {
  if (oldFiber.index > newIdx) {
    nextOldFiber = oldFiber;
    oldFiber = null;
  } else {
    nextOldFiber = oldFiber.sibling;
  }
  const newFiber = updateSlot(
    returnFiber,
    oldFiber,
    newChildren[newIdx],
    lanes
  );
  if (newFiber === null) {
    // a better way to communicate whether this was a miss or null,
    // boolean, undefined, etc.
    if (oldFiber === null) {
      oldFiber = nextOldFiber;
    }
    break;
  }
  if (shouldTrackSideEffects) {
    if (oldFiber && newFiber.alternate === null) {
      // We matched the slot, but we didn't reuse the existing fiber, so we
      // need to delete the existing child.
      deleteChild(returnFiber, oldFiber);
    }
  }
  lastPlacedIndex = placeChild(newFiber, lastPlacedIndex, newIdx);
  if (previousNewFiber === null) {
    // TODO: Move out of the loop. This only happens for the first run.
    resultingFirstChild = newFiber;
  } else {
    // TODO: Defer siblings if we're not at the right index for this slot.
    // I.e. if we had null values before, then we want to defer this
    // for each null value. However, we also don't want to call updateSlot
    // with the previous one.
    previousNewFiber.sibling = newFiber;
  }
  previousNewFiber = newFiber;
  oldFiber = nextOldFiber;
}

Oh man, what the heck is going on. Let’s go step by step, I’ve added the comments.

for (; oldFiber !== null && newIdx < newChildren.length; newIdx++) {
this loops through the new elements
by keeping track of oldFiber, looks similar to two-pointer algorithm
recall the problem where you are asked to merge two sorted array.
  if (oldFiber.index > newIdx) {
    nextOldFiber = oldFiber;
    oldFiber = null;
  } else {
    nextOldFiber = oldFiber.sibling;
  }
because children fibers are linked by sibling
index is to reveal its position in the array
here it says:
ideally both pointers move ahead and nothing changes right.
But considering there are cases of empty values,
which means index might not be exactly its position
(see my previous post about Empty values)
so if olderFiber.index is larger, meaning this new child is comparing to null.
notice this new child might be null as well
  const newFiber = updateSlot(
    returnFiber,
    oldFiber,
    newChildren[newIdx],
    lanes
  );
now we compare the old and the new, hopefully they could match
open the function updateSlot(), we can see that
if new child is empty value or its key doesn't match
then newFiber is null
  if (newFiber === null) {
if newFiber is null, we need to obviously
either find its original position or create a new one right?
so break here.
    // this is to revert the variable
    if (oldFiber === null) {
      oldFiber = nextOldFiber;
    }
    break;
  }
  if (shouldTrackSideEffects) {
    if (oldFiber && newFiber.alternate === null) {
now we have newFiber, if it is same type of oldFiber
then they should be connected with alternate
if not, meaning replacement, so need to delete the oldFiber.
      // We matched the slot, but we didn't reuse the existing fiber, so we
      // need to delete the existing child.
      deleteChild(returnFiber, oldFiber);
    }
  }
  lastPlacedIndex = placeChild(newFiber, lastPlacedIndex, newIdx);
We've successfully get a new fiber
we need to mark the fiber to tell React that
put its DOM node to thew new index.
lastPlacedIndex is very interesting, we'll cover it in details after this.
we need to chain the fibers up right?
so previousNewFiber allows us to do so.
  if (previousNewFiber === null) {
    resultingFirstChild = newFiber;
  } else {
    previousNewFiber.sibling = newFiber;
  }
  previousNewFiber = newFiber;
  oldFiber = nextOldFiber;
}

for (; oldFiber !== null && newIdx < newChildren.length; newIdx++) {
this loops through the new elements
by keeping track of oldFiber, looks similar to two-pointer algorithm
recall the problem where you are asked to merge two sorted array.
  if (oldFiber.index > newIdx) {
    nextOldFiber = oldFiber;
    oldFiber = null;
  } else {
    nextOldFiber = oldFiber.sibling;
  }
because children fibers are linked by sibling
index is to reveal its position in the array
here it says:
ideally both pointers move ahead and nothing changes right.
But considering there are cases of empty values,
which means index might not be exactly its position
(see my previous post about Empty values)
so if olderFiber.index is larger, meaning this new child is comparing to null.
notice this new child might be null as well
  const newFiber = updateSlot(
    returnFiber,
    oldFiber,
    newChildren[newIdx],
    lanes
  );
now we compare the old and the new, hopefully they could match
open the function updateSlot(), we can see that
if new child is empty value or its key doesn't match
then newFiber is null
  if (newFiber === null) {
if newFiber is null, we need to obviously
either find its original position or create a new one right?
so break here.
    // this is to revert the variable
    if (oldFiber === null) {
      oldFiber = nextOldFiber;
    }
    break;
  }
  if (shouldTrackSideEffects) {
    if (oldFiber && newFiber.alternate === null) {
now we have newFiber, if it is same type of oldFiber
then they should be connected with alternate
if not, meaning replacement, so need to delete the oldFiber.
      // We matched the slot, but we didn't reuse the existing fiber, so we
      // need to delete the existing child.
      deleteChild(returnFiber, oldFiber);
    }
  }
  lastPlacedIndex = placeChild(newFiber, lastPlacedIndex, newIdx);
We've successfully get a new fiber
we need to mark the fiber to tell React that
put its DOM node to thew new index.
lastPlacedIndex is very interesting, we'll cover it in details after this.
we need to chain the fibers up right?
so previousNewFiber allows us to do so.
  if (previousNewFiber === null) {
    resultingFirstChild = newFiber;
  } else {
    previousNewFiber.sibling = newFiber;
  }
  previousNewFiber = newFiber;
  oldFiber = nextOldFiber;
}

A bit clearer now right ? The key point to understand this piece of code are

1. why comparing oldFiber.index > newIdx
2. when newFiber will be null.

Anyway let’s continue, following part looks straightforward.

if (newIdx === newChildren.length) {
  // We've reached the end of the new children. We can delete the rest.
  deleteRemainingChildren(returnFiber, oldFiber);
  if (getIsHydrating()) {
    const numberOfForks = newIdx;
    pushTreeFork(returnFiber, numberOfForks);
  }
 
  return resultingFirstChild;
yeah, per name it returns the first child
because reconcileChildren is run for its parent
it the first child is needed to set workInProgress.child = reconcileChildFibers()code
notice that, reconcileChildren() is just preparation,
each child still needs to be reconciled.
}

if (newIdx === newChildren.length) {
  // We've reached the end of the new children. We can delete the rest.
  deleteRemainingChildren(returnFiber, oldFiber);
  if (getIsHydrating()) {
    const numberOfForks = newIdx;
    pushTreeFork(returnFiber, numberOfForks);
  }
 
  return resultingFirstChild;
yeah, per name it returns the first child
because reconcileChildren is run for its parent
it the first child is needed to set workInProgress.child = reconcileChildFibers()code
notice that, reconcileChildren() is just preparation,
each child still needs to be reconciled.
}

Continue

js
if (oldFiber === null) {
  // If we don't have any more existing children we can choose a fast path
  // since the rest will all be insertions.
  for (; newIdx < newChildren.length; newIdx++) {
    const newFiber = createChild(returnFiber, newChildren[newIdx], lanes);
    if (newFiber === null) {
      continue;
    }
    lastPlacedIndex = placeChild(newFiber, lastPlacedIndex, newIdx);
    if (previousNewFiber === null) {
      resultingFirstChild = newFiber;
    } else {
      previousNewFiber.sibling = newFiber;
    }
    previousNewFiber = newFiber;
  }
  return resultingFirstChild;
}

js
if (oldFiber === null) {
  // If we don't have any more existing children we can choose a fast path
  // since the rest will all be insertions.
  for (; newIdx < newChildren.length; newIdx++) {
    const newFiber = createChild(returnFiber, newChildren[newIdx], lanes);
    if (newFiber === null) {
      continue;
    }
    lastPlacedIndex = placeChild(newFiber, lastPlacedIndex, newIdx);
    if (previousNewFiber === null) {
      resultingFirstChild = newFiber;
    } else {
      previousNewFiber.sibling = newFiber;
    }
    previousNewFiber = newFiber;
  }
  return resultingFirstChild;
}

Last piece of puzzle

const existingChildren = mapRemainingChildren(returnFiber, oldFiber);
Since we still have new children to check
let's see if we can find the same key in existing fibers,
if found then we can use them for future reconciliation.
Add all children to a key map for quick lookups.
Here just change it back to Array.
Keep scanning and use the map to restore deleted items as moves.
for (; newIdx < newChildren.length; newIdx++) {
  // `updateFromMap` is like `updateSlot`
  // but try to get fiber from the fiber map
  const newFiber = updateFromMap(
    existingChildren,
    returnFiber,
    newIdx,
    newChildren[newIdx],
    lanes
  );
  if (newFiber !== null) {
    // handle deletion again.
    if (shouldTrackSideEffects) {
      if (newFiber.alternate !== null) {
        existingChildren.delete(newFiber.key === null ? newIdx : newFiber.key);
      }
    }
    lastPlacedIndex = placeChild(newFiber, lastPlacedIndex, newIdx);
    if (previousNewFiber === null) {
      resultingFirstChild = newFiber;
    } else {
      previousNewFiber.sibling = newFiber;
    }
    previousNewFiber = newFiber;
  }
}
if (shouldTrackSideEffects) {
  // Any existing children that weren't consumed above were deleted. We need
  // to add them to the deletion list.
  existingChildren.forEach((child) => deleteChild(returnFiber, child));
}
return resultingFirstChild;

const existingChildren = mapRemainingChildren(returnFiber, oldFiber);
Since we still have new children to check
let's see if we can find the same key in existing fibers,
if found then we can use them for future reconciliation.
Add all children to a key map for quick lookups.
Here just change it back to Array.
Keep scanning and use the map to restore deleted items as moves.
for (; newIdx < newChildren.length; newIdx++) {
  // `updateFromMap` is like `updateSlot`
  // but try to get fiber from the fiber map
  const newFiber = updateFromMap(
    existingChildren,
    returnFiber,
    newIdx,
    newChildren[newIdx],
    lanes
  );
  if (newFiber !== null) {
    // handle deletion again.
    if (shouldTrackSideEffects) {
      if (newFiber.alternate !== null) {
        existingChildren.delete(newFiber.key === null ? newIdx : newFiber.key);
      }
    }
    lastPlacedIndex = placeChild(newFiber, lastPlacedIndex, newIdx);
    if (previousNewFiber === null) {
      resultingFirstChild = newFiber;
    } else {
      previousNewFiber.sibling = newFiber;
    }
    previousNewFiber = newFiber;
  }
}
if (shouldTrackSideEffects) {
  // Any existing children that weren't consumed above were deleted. We need
  // to add them to the deletion list.
  existingChildren.forEach((child) => deleteChild(returnFiber, child));
}
return resultingFirstChild;

Phew, that’s a lot of code, but we managed to cover it. Do you feel more familiar with it now?

Wait, we still need to talk about placeChild().

function placeChild(
  newFiber: Fiber,
  lastPlacedIndex: number,
  newIndex: number
): number {
  newFiber.index = newIndex;
  const current = newFiber.alternate;
  if (current !== null) {
if current is not null, meaning it might be a move
    const oldIndex = current.index;
    if (oldIndex < lastPlacedIndex) {
if oldIndex is smaller, meaning it is move
      newFiber.flags |= Placement;
      return lastPlacedIndex;
return the old lastPlacedIndex, meaning it won't increment
    } else {
      // This item can stay in place.
      // return the index, which should increment.
      return oldIndex;
    }
  } else {
    // This is an insertion.
    newFiber.flags |= Placement;
    return lastPlacedIndex;
  }
}

function placeChild(
  newFiber: Fiber,
  lastPlacedIndex: number,
  newIndex: number
): number {
  newFiber.index = newIndex;
  const current = newFiber.alternate;
  if (current !== null) {
if current is not null, meaning it might be a move
    const oldIndex = current.index;
    if (oldIndex < lastPlacedIndex) {
if oldIndex is smaller, meaning it is move
      newFiber.flags |= Placement;
      return lastPlacedIndex;
return the old lastPlacedIndex, meaning it won't increment
    } else {
      // This item can stay in place.
      // return the index, which should increment.
      return oldIndex;
    }
  } else {
    // This is an insertion.
    newFiber.flags |= Placement;
    return lastPlacedIndex;
  }
}

It is a bit hard to understand the code here. We keep in mind that

1. for insertion, the fibers are newly created, Placement means the DOM node will be collected.
2. if it is move, Also it must be moved backward or forward
   • if backward, we don’t need to do anything, because fibers before it would go away, leaving it to the right position.
   • if forward, we need to do real move. Placement will move them because appendChild() does it natively.

I’ve draw an illustration for this, suppose we have order changes like below

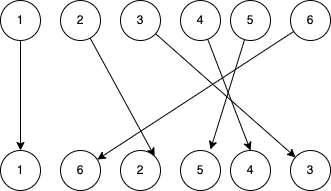
6 actually could be kept unmoved, because the after 2, 5, 4, 3, are moved, 6 will be automatically placed as sibling to 1.

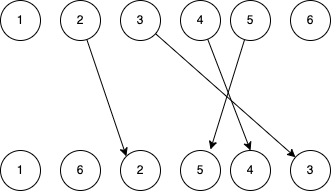
You might wonder why not do the opposite, like inserting 6 before 2. Remember we are creating a linked list, we cannot know a fiber’s sibling while processing the fiber. That’s why for 6 above, we only set 2 as its sibling when processing 2.

For above case, lastPlacedIndex is

1. first set to 0, but find position not change, so no need to move. return 0
2. comparing 6, moving backward, no need to move. return 5
3. comparing 2, old index is 1 , smaller than 5, moving forward
4. comparing 5, old index is 4 , smaller than 5, moving forward
5. comparing 4, old index is 3 , smaller than 5, moving forward
6. comparing 3, old index is 2 , smaller than 5, moving forward

BTW, the code behind Placement is in the commit phase. (source)

It is pretty straightforward.

js
function insertOrAppendPlacementNode(
  node: Fiber,
  before: ?Instance,
  parent: Instance
): void {
  const { tag } = node;
  const isHost = tag === HostComponent || tag === HostText;
  if (isHost) {
    const stateNode = node.stateNode;
    if (before) {
      insertBefore(parent, stateNode, before);
    } else {
      appendChild(parent, stateNode);
    }
  } else if (tag === HostPortal) {
    // If the insertion itself is a portal, then we don't want to traverse
    // down its children. Instead, we'll get insertions from each child in
    // the portal directly.
  } else {
    const child = node.child;
    if (child !== null) {
      insertOrAppendPlacementNode(child, before, parent);
      let sibling = child.sibling;
      while (sibling !== null) {
        insertOrAppendPlacementNode(sibling, before, parent);
        sibling = sibling.sibling;
      }
    }
  }
}

js
function insertOrAppendPlacementNode(
  node: Fiber,
  before: ?Instance,
  parent: Instance
): void {
  const { tag } = node;
  const isHost = tag === HostComponent || tag === HostText;
  if (isHost) {
    const stateNode = node.stateNode;
    if (before) {
      insertBefore(parent, stateNode, before);
    } else {
      appendChild(parent, stateNode);
    }
  } else if (tag === HostPortal) {
    // If the insertion itself is a portal, then we don't want to traverse
    // down its children. Instead, we'll get insertions from each child in
    // the portal directly.
  } else {
    const child = node.child;
    if (child !== null) {
      insertOrAppendPlacementNode(child, before, parent);
      let sibling = child.sibling;
      while (sibling !== null) {
        insertOrAppendPlacementNode(sibling, before, parent);
        sibling = sibling.sibling;
      }
    }
  }
}

That’s it. The diffing algorithm is actually not very complex, hope this posts could help you understand.

Want to know more about how React works internally?
Check out my series - React Internals Deep Dive!